Contoh Soal Dan Pembahasan Ihwal Persamaan Bulat Sma
Jika dikala SD dan Sekolah Menengah Pertama kalian sudah dikenalkan dengan lingkaran, maka di Sekolah Menengan Atas kalian akan mempelajari bulat lagi. Tapi, di Sekolah Menengan Atas materinya persamaan lingkaran, yuk cek teladan soal dan pembahasannya:
1. Persamaan bulat berpusat di titik (2, 3) dan melalui titik (5, -1) adalah...
Pembahasan:
Persamaan bulat yang berpusat di (2, 3) dan melalui titik (5, -1)adalah:
r = √25
r = 5
sehingga persamaan lingkarannya:
jawaban: A
2. Persamaan garis singgung bulat
di titik (7, 1) adalah...
a. 3x – 4y – 41 = 0
b. 4x + 3y – 55 = 0
c. 4x – 5y – 53 = 0
d. 4x + 3y – 31 = 0
e. 4x – 3y – 40 = 0
Pembahasan:
Persamaan garis singgung bulat melalui titik (x1, y1) dicari dengan rumus:
x1.x + y1.y + a(x1 + x) + b (y1 + y) + c = 0
x1.x + y1.y – ½ . 6 (x1 + x) + ½ . 4 (y1 + y) - 12 = 0
7.x + 1.y – 3 (7 + x) + 2 (1 + y) - 12 = 0
7x + y – 21 – 3x + 2 + 2y – 12 = 0
4x + 3y – 31 = 0
Jawaban: D
3. Lingkaran
memotong garis y = 1. Persamaan garis singgung di titik potong bulat dan garis y = 1 ialah ...
a. x = 2 dan x = 4
b. x = 3 dan x = 1
c. x = 1 dan x = 5
d. x = 2 dan x = 3
e. x = 3 dan x = 4
pembahasan:
Lingkaran memotong garis y = 1 di titik:
x = 2 dan x = 4
jadi, titik potongnya (2, 1) dan (4, 1)
persamaan lingkarannya menjadi:
persamaan garis singgung terhadap bulat L melalui titik (2, 1) adalah:
x1.x + y1.y + a(x1 + x) + b (y1 + y) + c = 0
x1.x + y1.y – ½ . 6 (x1 + x) - ½ . 2 (y1 + y) + 9 = 0
2.x + 1.y – 3 (2 + x) - 1 (1 + y) + 9 = 0
2x + y – 6 – 3x – 1 – y + 9 = 0
-x + 2 = 0
x = 2
persamaan garis singgung terhadap bulat L melalui titik (4, 1) adalah:
x1.x + y1.y + a(x1 + x) + b (y1 + y) + c = 0
x1.x + y1.y – ½ . 6 (x1 + x) - ½ . 2 (y1 + y) + 9 = 0
4.x + 1.y – 3 (4 + x) - 1 (1 + y) + 9 = 0
4x + y – 12 – 3x – 1 – y + 9 = 0
x - 4 = 0
x = 4
jawaban: A
4. persamaan bulat dengan sentra (3 , -2) dan menyinggung sumbu Y ialah ...
Pembahasan:
Rumus persamaan bulat dengan sentra (a, b) adalah:
Karena, garis menyinggung sumbu y, maka jari-jari = x = 3 (karena pusatnya (3, -2), sehingga:
jawaban: D
5. Jarak antara titik sentra bulat
dari sumbu y ialah ...
a. 3
b. 2,5
c. 2
d. 1,5
e. 1
Pembahasan:
Lingkaran dengan persamaan
memiliki titik sentra ( -a, -b), maka:
( - ½ .(-4) , - ½ . (0)) = (2, 0)
Karena, titik pusatnya (2, 0) maka jarak bulat ke sumbu y = x = 2
Jawaban: C
6. Lingkaran
menyinggung garis x = 4 di titik ...
a. (4, 6)
b. (4, -6)
c. (4, 4)
d. (4, 1)
e. (4, -1)
Pembahasan:
Lingkaran menyinggung garis x = 4 maka:
(y + 1) (y + 1) = 0
y = -1
jadi, bulat menyinggung di titik ( 4, -1)
jawaban: E
7. Lingkaran yang sepusat dengan bulat
dan menyinggung garis 3x – 4y + 7 = 0 mempunyai persamaan ...
Pembahasan:
Lingkaran dengan persamaan mempunyai titik sentra ( -a, -b), maka:
( - ½ . (-4), - ½ . 6) = ( 2, -3)
Sehingga persamaan garis yang berpusat di (2, -3) adalah:
Panjang jari-jari (r) bulat ialah jarak titik sentra (2, -3) ke garis 3x – 4y + 7 = 0, maka:
jadi, persamaan lingkarannya menjadi:
Jawaban: A
8. Diketahui bulat
mempunyai jari-jari 5 dan menyinggung sumbu x. Pusat bulat tersebut ialah ...
a. (-5, -3)
b. (-5, 3)
c. (6, -5)
d. (-6, -5)
e. (3, -5)
Pembahasan:
Rumus jari-jari adalah:
maka:
p = ± 3
sehingga persamaannya menjadi:
Titik pusatnya = (- ½ .6 , - ½ .10) = (-3, -5)
Titik pusatnya = (- ½ .(-6) , - ½ .10) = (3, -5)
Jawaban: E
9. Persamaan garis singgung melalui titik (5, 1) pada bulat
adalah ...
a. 3x + 4y – 19 = 0
b. 3x - 4y – 19 = 0
c. 4x - 3y + 19 = 0
d. x + 7y – 26 = 0
e. x - 7y – 26 = 0
pembahasan:
persamaan garis singgung terhadap bulat melalui titik (5, 1) adalah:
x1.x + y1.y + a(x1 + x) + b (y1 + y) + c = 0
5.x + 1.y + ½ .(-4) (5 + x) + ½ .6 (1 + y) - 12 = 0
5x + y + -2 (5 + x) + 3 (1 + y) - 12 = 0
5x + y – 10 – 2x + 3 + 3y – 12 = 0
3x + 4y - 19 = 0
Jawaban: A
10. bulat dengan persamaan
melalui titik (5, -1). Jari-jarinya adalah...
a. √7
b. 3
c. 4
d. 2√6
e. 9
Pembahasan:
Lingkaran melalui (5, -1) maka:
25 + 1 – 20 – 2 + c = 0
4 + c = 0
c = -4
sehingga jari-jari lingkarannya:
r = 3
jawaban: B
11. Lingkaran
mempunyai jari-jari 3 dan menyinggung sumbu x. Pusat bulat tersebut sama dengan ...
a. (-2, 3)
b. (2, -3)
c. (2, 3)
d. (3, -2)
e. (-3, 2)
Pembahasan:
p = ± 2
sehingga persamaannya menjadi:
Pusatnya: (- ½ .4, - ½ .6) = (-2, -3)
Pusatnya: (- ½ . (-4), - ½ . 6) = ( 2, -3)
Jawaban: B
12. Persamaan garis singgung pada bulat
yang tegak lurus garis 5x – 12y + 15 = 0 ialah ...
a. 12x + 5y – 41 = 0 dan 12x + 5y + 37 = 0
b. 12x + 5y + 41 = 0 dan 12x + 5y + 37 = 0
c. 5x + 12y + 41 = 0 dan 5x + 12y + 37 = 0
d. 5x + 12y - 41 = 0 dan 5x + 12y - 37 = 0
e. 12x - 5y – 41 = 0 dan 12x - 5y - 37 = 0
Pembahasan:
Pusat lingkaran: ( - ½ .(-2), - ½ .4) = ( 1, -2)
r = 3
garis 5x – 12y + 15 = 0 mempunyai gradien m = -a/b = -5/-12 = 5/12 sebab garis yang ditanyakan ialah garis yang tegak lurus, maka gradiennya menjadi: -12/5
persamaan garis singgung bulat dengan sentra (a, b) ; berjari-jari r; dan bergradien m adalah:
Karena sentra lingkarannya (1, -2); r = 3, dan m = -12/5 , maka:
(y + 2) = -12/5 (x – 1) ± 3 .13/5 (kalikan 5)
5 (y + 2) = 5 .-12/5 (x – 1) ± 5.3 .13/5
5y + 10 = -12 (x – 1) ± 15 . 13/5
5y + 10 = -12x + 12 ± 39
12x + 5y – 2 ± 39 = 0
Jadi, persamaan garis singgungnya:
12x + 5y – 2 + 39 = 0 ==> 12x + 5y + 37 = 0, dan
12x + 5y – 2 - 39 = 0 ==> 12x + 5y – 41 = 0
Jawaban: A
13. Persamaan bulat yang mempunyai diameter AB dengan A (-2, 2) dan B (2, -2) ialah ...
Pembahasan:
Jari-jari = ½ diameter
r = ½ √32
r = ½.4 √2
r = 2√2
pusat lingkaran:
persamaan lingkarannya:
jawaban: C
14. Garis x + y = 2 menyinggung bulat
untuk q = ...
a. -8
b. 4
c. 6
d. 8
e. 16
Pembahasan:
Pusat bulat = (- ½ .(-6), - ½ (-2)) = (3, 1)
Jarak titik sentra (3,1) bulat dengan dengan garis x + y = 2 atau x + y – 2 = 0adalah r, maka:
2 = 10 – q
q = 8
jawaban: D
15. Jika bulat
yang berpusat di titik (2, 3) menyinggung garis y = 1 – x maka nilai c sama dengan ...
a. 0
b. 4
c. 5
d. 9
e. 13
Pembahasan:
Garis garis y = 1 – x menyinggung lingkaran, maka:
Syarat menyinggung ialah D = 0, maka:
0 – 4. 2. (-5 + c) = 0
40 – 8c = 0
8c = 40
c = 5
Jawaban: C
16. Persamaan garis singgung melalui titik (0, 5) pada bulat
ialah ...
a. 2x + y = 10 dan -2x + y = 10
b. x + 2y = 10 dan x - 2y = -10
c. x + 2y = 10 dan x - 2y = 10
d. x + y = -10 dan 2x - y = 10
e. x + 2y = -10 dan x - 2y = -10
Pembahasan:
Kita subtitusikan titik (0, 5) dalam:
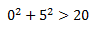sebab nilainya lebih besar, maka titik (0, 5) berada di luar lingkaran.
Persamaan garis yang melalui titik (0, 5) adalah:
y – y1 = m (x – x1)
y – 5 = m (x – 0)
y = mx + 5
kita subtitusikan y = mx + 5 pada persamaan:
Karena y = mx + 5 menyinggung lingkaran, maka D = 0
m = ± ½
2y = x + 10 atau x – 2y = 10
2y = -x + 10 atau x + 2y = 10
Jawaban: B
17. Supaya garis y = x + a menyinggung bulat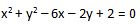
haruslah ...
a. a = -6 atau a = 1
b. a = -5 atau a = 2
c. a = -1 atau a = 1
d. a = -6 atau a = 2
e. a = 6 atau a = -2
Pembahasan:
Garis y = x + a menyinggung lingkaran, maka:
Syarat menyinggung, D = 0
(-a – 6) (a – 2) = 0
a = -6 atau a = 2
jawaban: D
18. Salah satu persamaan garis singgung yang ditarik dari titik A (0, 10) ke bulat yang persamaannya
adalah ...
a. y = 10x + 3
b. y = 10x - 3
c. y = 3x - 10
d. y = -3x - 10
e. y = -3x +10
pembahasan:
mempunyai titik sentra (0, 0) dan jari-jari √10
Persamaan garis singgung bergradien m adalah:
Garis singgungnya melalui titik (0, 10), maka:
m = ± 3
Persamaan garis singgungnya menjadi:
y – 10 = 3 (x – 0)
y = 3x + 10
y – 10 = -3 (x – 0)
y = -3x + 10
Jawaban: E
19. titik sentra bulat L yang berada di kuadran I dan berada di sepanjang garis y = 2x. Jika L menyinggung sumbu y di titik (0, 6) maka persamaan L ialah ..
Pembahasan:
Ketika y = 6, maka y = 2x, maka x = 3
Sehingg sentra lingkarannya ialah (3, 6) dengan jari-jari = r = x = 3
Maka, persamaan lingkarannya menjadi:
Jawaban: E
20. Lingkaran yang sepusat dengan bulat
dan menyinggung garis 3x – 4y + 7 = 0 mempunyai persamaan ...
Pembahasan:
Pusat bulat = (- ½ .(-4), - ½ .6) = (2, -3)
Lingkaran menyinggung garis 3x – 4y + 7 = 0 maka jari-jarinya adalah:
r = 5
persamaan lingkarannya adalah:
Jawaban: A
21. Jika A (1, 3), B (7, -5) maka persamaan bulat yang mempunyai diameter AB ialah ...
Pembahasan:
Titik pusat:
Panjang jari-jari sama dengan jarak A ke B atau B ke titik pusat:
Jadi, persamaan bulat dengan sentra (4, -1) dan jari-jari 5 adalah:
Jawaban: A
22. Diketahui suatu bulat dengan sentra berada pada kurva y = √x dan melalui titik asal O (0, 0). Jika absis titik sentra bulat terseut ialah a, maka persamaan garis singgung bulat yang melalui O ialah ...
a. y = -x
b. y = -x√a
c. y = -ax
d. y = -2x√2
e. y = -2ax
Pembahasan:
x = a, maka y = √x = √a sehingga titik pusatnya ialah (a, √a)
persamaan lingkarannya:
Lingkaran melalui titik O (0, 0), maka:
sehingga diperoleh
persamaan garis singgung bulat
dan melalui O (0, 0) adalah:
Jawaban: B
23. bulat
yang pusatnya berimpitan dengan sentra dan berjari-jari 5, memotong sumbu x dan sumbu y konkret di titik (a, 0) dan (0, b). Nilai ab = ...
a. 10√6 – 15
b. 10√5 - 15
c. 8√6 - 10
d. 8√5 - 10
e. 15/2 √6-10
Pembahasan:
Pusat bulat = (- ½ . (-2), - ½ . 6) = (1, -3)
Persamaan bulat dengan sentra (1, -3) dan jari-jari 5 adalah:
Lingkaran memotong sumbu x positif, maka y = 0
x – 1 = √16
x – 1 = 4
x = 5
a = 5
lingkaran memotong sumbu y positif, maka x = 0
y + 3 = √24
y = √24 – 3
b = √24 – 3
jadi, nilai ab = 5 (√24 – 3) = 5 (√4.6 – 3) = 10√6 - 15
Jawaban: A
24. Jari-jari bulat pada gambar di bawah ini ialah ...
a. √3
b. 3
c. √13
d. 3√3
e. √37
Pembahasan:
Bentuk umum persamaan bulat ialah
25 + 5A + C = 0 atau,
5A + C = -25 ... (i)
25 + 5B + C = 0
5B + C = -25 ... (ii)
1 – A + C = 0
-A + C = -1 ... (iii)
Eliminasi (i) dan (iii)
A = -4
Subtitusikan A = -4, pada persamaan –A + C = -1
-(-4) + C = -1
C = -5
Subtitusikan C = -5 pada persamaan 5B + C = -25
5B + (-5) = -25
5B = -20
B = -4
Sehingga persamaan lingkarannya menjadi:
Jari-jarinya:
r = √13
Jawaban: C
25. Salah satu garis singgung yang bersudut 120 derajat terhadap sumbu x konkret pada bulat dengan ujung diameter di titik (7, 6) dan (1, -2) ialah ...
a. y = -x√3 + 4√3 + 12
b. y = -x√3 - 4√3 + 8
c. y = -x√3 + 4√3 + 8
d. y = -x√3 - 4√3 - 8
e y = -x√3 + 4√3 + 22
Pembahasan:
Jari-jari:
Titik pusat:
Persamaan lingkarannya:
Persamaan garis singgung lingkaran:
...(i)
Perhatikan gambar garis singgung yang dimaksud:
Berdasarkan gambar di atas, gradien garis yang dimaksud ialah y/x = - √3 /1 = - √3
Maka persamaan garis singgungnya (i) menjadi:
y = - x√3 + 4 √3 ± 5√4 + 2
y = - x√3 + 4 √3 ± 10 + 2
y = - x√3 + 4 √3 ± 10 + 2
y = - x√3 + 4 √3 + 10 + 2 = - x√3 + 4 √3 + 12
y = - x√3 + 4 √3 - 10 + 2 = - x√3 + 4 √3 - 8
Jawaban: A
Gimana nih adik-adik? sehabis mencar ilmu bersama kakak, makin paham atau makin galau nih? hehehe... biar bermanfaat ya, jangan putus-putus latihannya...
1. Persamaan bulat berpusat di titik (2, 3) dan melalui titik (5, -1) adalah...
Pembahasan:Persamaan bulat yang berpusat di (2, 3) dan melalui titik (5, -1)adalah:
r = √25
r = 5
sehingga persamaan lingkarannya:
jawaban: A
2. Persamaan garis singgung bulat
di titik (7, 1) adalah...a. 3x – 4y – 41 = 0
b. 4x + 3y – 55 = 0
c. 4x – 5y – 53 = 0
d. 4x + 3y – 31 = 0
e. 4x – 3y – 40 = 0
Pembahasan:
Persamaan garis singgung bulat
melalui titik (x1, y1) dicari dengan rumus:x1.x + y1.y + a(x1 + x) + b (y1 + y) + c = 0
x1.x + y1.y – ½ . 6 (x1 + x) + ½ . 4 (y1 + y) - 12 = 0
7.x + 1.y – 3 (7 + x) + 2 (1 + y) - 12 = 0
7x + y – 21 – 3x + 2 + 2y – 12 = 0
4x + 3y – 31 = 0
Jawaban: D
3. Lingkaran
memotong garis y = 1. Persamaan garis singgung di titik potong bulat dan garis y = 1 ialah ...a. x = 2 dan x = 4
b. x = 3 dan x = 1
c. x = 1 dan x = 5
d. x = 2 dan x = 3
e. x = 3 dan x = 4
pembahasan:
Lingkaran
memotong garis y = 1 di titik:x = 2 dan x = 4
jadi, titik potongnya (2, 1) dan (4, 1)
persamaan lingkarannya menjadi:
persamaan garis singgung terhadap bulat L melalui titik (2, 1) adalah:
x1.x + y1.y + a(x1 + x) + b (y1 + y) + c = 0
x1.x + y1.y – ½ . 6 (x1 + x) - ½ . 2 (y1 + y) + 9 = 0
2.x + 1.y – 3 (2 + x) - 1 (1 + y) + 9 = 0
2x + y – 6 – 3x – 1 – y + 9 = 0
-x + 2 = 0
x = 2
persamaan garis singgung terhadap bulat L melalui titik (4, 1) adalah:
x1.x + y1.y + a(x1 + x) + b (y1 + y) + c = 0
x1.x + y1.y – ½ . 6 (x1 + x) - ½ . 2 (y1 + y) + 9 = 0
4.x + 1.y – 3 (4 + x) - 1 (1 + y) + 9 = 0
4x + y – 12 – 3x – 1 – y + 9 = 0
x - 4 = 0
x = 4
jawaban: A
4. persamaan bulat dengan sentra (3 , -2) dan menyinggung sumbu Y ialah ...
Pembahasan:
Rumus persamaan bulat dengan sentra (a, b) adalah:
Karena, garis menyinggung sumbu y, maka jari-jari = x = 3 (karena pusatnya (3, -2), sehingga:
jawaban: D
5. Jarak antara titik sentra bulat
dari sumbu y ialah ...a. 3
b. 2,5
c. 2
d. 1,5
e. 1
Pembahasan:
Lingkaran dengan persamaan
memiliki titik sentra ( -a, -b), maka:( - ½ .(-4) , - ½ . (0)) = (2, 0)
Karena, titik pusatnya (2, 0) maka jarak bulat ke sumbu y = x = 2
Jawaban: C
6. Lingkaran
menyinggung garis x = 4 di titik ...a. (4, 6)
b. (4, -6)
c. (4, 4)
d. (4, 1)
e. (4, -1)
Pembahasan:
Lingkaran
menyinggung garis x = 4 maka:(y + 1) (y + 1) = 0
y = -1
jadi, bulat menyinggung di titik ( 4, -1)
jawaban: E
7. Lingkaran yang sepusat dengan bulat
dan menyinggung garis 3x – 4y + 7 = 0 mempunyai persamaan ... Pembahasan:
Lingkaran dengan persamaan
mempunyai titik sentra ( -a, -b), maka:( - ½ . (-4), - ½ . 6) = ( 2, -3)
Sehingga persamaan garis yang berpusat di (2, -3) adalah:
Panjang jari-jari (r) bulat ialah jarak titik sentra (2, -3) ke garis 3x – 4y + 7 = 0, maka:
jadi, persamaan lingkarannya menjadi:
Jawaban: A
8. Diketahui bulat
mempunyai jari-jari 5 dan menyinggung sumbu x. Pusat bulat tersebut ialah ...a. (-5, -3)
b. (-5, 3)
c. (6, -5)
d. (-6, -5)
e. (3, -5)
Pembahasan:
Rumus jari-jari adalah:
maka:p = ± 3
sehingga persamaannya menjadi:
Titik pusatnya = (- ½ .6 , - ½ .10) = (-3, -5)
Titik pusatnya = (- ½ .(-6) , - ½ .10) = (3, -5)
Jawaban: E
9. Persamaan garis singgung melalui titik (5, 1) pada bulat
adalah ...
a. 3x + 4y – 19 = 0
b. 3x - 4y – 19 = 0
c. 4x - 3y + 19 = 0
d. x + 7y – 26 = 0
e. x - 7y – 26 = 0
pembahasan:
persamaan garis singgung terhadap bulat melalui titik (5, 1) adalah:
x1.x + y1.y + a(x1 + x) + b (y1 + y) + c = 0
5.x + 1.y + ½ .(-4) (5 + x) + ½ .6 (1 + y) - 12 = 0
5x + y + -2 (5 + x) + 3 (1 + y) - 12 = 0
5x + y – 10 – 2x + 3 + 3y – 12 = 0
3x + 4y - 19 = 0
Jawaban: A
10. bulat dengan persamaan
melalui titik (5, -1). Jari-jarinya adalah...a. √7
b. 3
c. 4
d. 2√6
e. 9
Pembahasan:
Lingkaran
melalui (5, -1) maka:25 + 1 – 20 – 2 + c = 0
4 + c = 0
c = -4
sehingga jari-jari lingkarannya:
r = 3
jawaban: B
11. Lingkaran
mempunyai jari-jari 3 dan menyinggung sumbu x. Pusat bulat tersebut sama dengan ...a. (-2, 3)
b. (2, -3)
c. (2, 3)
d. (3, -2)
e. (-3, 2)
Pembahasan:
p = ± 2
sehingga persamaannya menjadi:
Pusatnya: (- ½ .4, - ½ .6) = (-2, -3)
Pusatnya: (- ½ . (-4), - ½ . 6) = ( 2, -3)
Jawaban: B
12. Persamaan garis singgung pada bulat
yang tegak lurus garis 5x – 12y + 15 = 0 ialah ...a. 12x + 5y – 41 = 0 dan 12x + 5y + 37 = 0
b. 12x + 5y + 41 = 0 dan 12x + 5y + 37 = 0
c. 5x + 12y + 41 = 0 dan 5x + 12y + 37 = 0
d. 5x + 12y - 41 = 0 dan 5x + 12y - 37 = 0
e. 12x - 5y – 41 = 0 dan 12x - 5y - 37 = 0
Pembahasan:
Pusat lingkaran: ( - ½ .(-2), - ½ .4) = ( 1, -2)
r = 3
garis 5x – 12y + 15 = 0 mempunyai gradien m = -a/b = -5/-12 = 5/12 sebab garis yang ditanyakan ialah garis yang tegak lurus, maka gradiennya menjadi: -12/5
persamaan garis singgung bulat dengan sentra (a, b) ; berjari-jari r; dan bergradien m adalah:
Karena sentra lingkarannya (1, -2); r = 3, dan m = -12/5 , maka:
(y + 2) = -12/5 (x – 1) ± 3 .13/5 (kalikan 5)
5 (y + 2) = 5 .-12/5 (x – 1) ± 5.3 .13/5
5y + 10 = -12 (x – 1) ± 15 . 13/5
5y + 10 = -12x + 12 ± 39
12x + 5y – 2 ± 39 = 0
Jadi, persamaan garis singgungnya:
12x + 5y – 2 + 39 = 0 ==> 12x + 5y + 37 = 0, dan
12x + 5y – 2 - 39 = 0 ==> 12x + 5y – 41 = 0
Jawaban: A
13. Persamaan bulat yang mempunyai diameter AB dengan A (-2, 2) dan B (2, -2) ialah ...
Pembahasan:
Jari-jari = ½ diameter
r = ½ √32
r = ½.4 √2
r = 2√2
pusat lingkaran:
persamaan lingkarannya:
jawaban: C
14. Garis x + y = 2 menyinggung bulat
untuk q = ...a. -8
b. 4
c. 6
d. 8
e. 16
Pembahasan:
Pusat bulat = (- ½ .(-6), - ½ (-2)) = (3, 1)
Jarak titik sentra (3,1) bulat dengan dengan garis x + y = 2 atau x + y – 2 = 0adalah r, maka:
2 = 10 – q
q = 8
jawaban: D
15. Jika bulat
yang berpusat di titik (2, 3) menyinggung garis y = 1 – x maka nilai c sama dengan ...a. 0
b. 4
c. 5
d. 9
e. 13
Pembahasan:
Garis garis y = 1 – x menyinggung lingkaran, maka:
Syarat menyinggung ialah D = 0, maka:
0 – 4. 2. (-5 + c) = 0
40 – 8c = 0
8c = 40
c = 5
Jawaban: C
16. Persamaan garis singgung melalui titik (0, 5) pada bulat
ialah ...a. 2x + y = 10 dan -2x + y = 10
b. x + 2y = 10 dan x - 2y = -10
c. x + 2y = 10 dan x - 2y = 10
d. x + y = -10 dan 2x - y = 10
e. x + 2y = -10 dan x - 2y = -10
Pembahasan:
Kita subtitusikan titik (0, 5) dalam
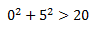: sebab nilainya lebih besar, maka titik (0, 5) berada di luar lingkaran.Persamaan garis yang melalui titik (0, 5) adalah:
y – y1 = m (x – x1)
y – 5 = m (x – 0)
y = mx + 5
kita subtitusikan y = mx + 5 pada persamaan
:Karena y = mx + 5 menyinggung lingkaran, maka D = 0
m = ± ½
- bila m = ½ maka:
2y = x + 10 atau x – 2y = 10
- bila m = - ½ maka:
2y = -x + 10 atau x + 2y = 10
Jawaban: B
17. Supaya garis y = x + a menyinggung bulat
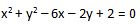haruslah ...a. a = -6 atau a = 1
b. a = -5 atau a = 2
c. a = -1 atau a = 1
d. a = -6 atau a = 2
e. a = 6 atau a = -2
Pembahasan:
Garis y = x + a menyinggung lingkaran, maka:
Syarat menyinggung, D = 0
(-a – 6) (a – 2) = 0
a = -6 atau a = 2
jawaban: D
18. Salah satu persamaan garis singgung yang ditarik dari titik A (0, 10) ke bulat yang persamaannya
adalah ...a. y = 10x + 3
b. y = 10x - 3
c. y = 3x - 10
d. y = -3x - 10
e. y = -3x +10
pembahasan:
mempunyai titik sentra (0, 0) dan jari-jari √10 Persamaan garis singgung bergradien m adalah:
Garis singgungnya melalui titik (0, 10), maka:
m = ± 3
Persamaan garis singgungnya menjadi:
- bila m = 3
y – 10 = 3 (x – 0)
y = 3x + 10
- bila m = -3
y – 10 = -3 (x – 0)
y = -3x + 10
Jawaban: E
19. titik sentra bulat L yang berada di kuadran I dan berada di sepanjang garis y = 2x. Jika L menyinggung sumbu y di titik (0, 6) maka persamaan L ialah ..
Pembahasan:
Ketika y = 6, maka y = 2x, maka x = 3
Sehingg sentra lingkarannya ialah (3, 6) dengan jari-jari = r = x = 3
Maka, persamaan lingkarannya menjadi:
Jawaban: E
20. Lingkaran yang sepusat dengan bulat
dan menyinggung garis 3x – 4y + 7 = 0 mempunyai persamaan ...Pembahasan:
Pusat bulat = (- ½ .(-4), - ½ .6) = (2, -3)
Lingkaran menyinggung garis 3x – 4y + 7 = 0 maka jari-jarinya adalah:
r = 5
persamaan lingkarannya adalah:
Jawaban: A
21. Jika A (1, 3), B (7, -5) maka persamaan bulat yang mempunyai diameter AB ialah ...
Pembahasan:
Titik pusat:
Panjang jari-jari sama dengan jarak A ke B atau B ke titik pusat:
Jadi, persamaan bulat dengan sentra (4, -1) dan jari-jari 5 adalah:
Jawaban: A
22. Diketahui suatu bulat dengan sentra berada pada kurva y = √x dan melalui titik asal O (0, 0). Jika absis titik sentra bulat terseut ialah a, maka persamaan garis singgung bulat yang melalui O ialah ...
a. y = -x
b. y = -x√a
c. y = -ax
d. y = -2x√2
e. y = -2ax
Pembahasan:
x = a, maka y = √x = √a sehingga titik pusatnya ialah (a, √a)
persamaan lingkarannya:
Lingkaran melalui titik O (0, 0), maka:
sehingga diperoleh
persamaan garis singgung bulat
dan melalui O (0, 0) adalah:Jawaban: B
23. bulat
yang pusatnya berimpitan dengan sentra dan berjari-jari 5, memotong sumbu x dan sumbu y konkret di titik (a, 0) dan (0, b). Nilai ab = ...a. 10√6 – 15
b. 10√5 - 15
c. 8√6 - 10
d. 8√5 - 10
e. 15/2 √6-10
Pembahasan:
Pusat bulat = (- ½ . (-2), - ½ . 6) = (1, -3)
Persamaan bulat dengan sentra (1, -3) dan jari-jari 5 adalah:
Lingkaran memotong sumbu x positif, maka y = 0
x – 1 = √16
x – 1 = 4
x = 5
a = 5
lingkaran memotong sumbu y positif, maka x = 0
y + 3 = √24
y = √24 – 3
b = √24 – 3
jadi, nilai ab = 5 (√24 – 3) = 5 (√4.6 – 3) = 10√6 - 15
Jawaban: A
24. Jari-jari bulat pada gambar di bawah ini ialah ...
a. √3
b. 3
c. √13
d. 3√3
e. √37
Pembahasan:
Bentuk umum persamaan bulat ialah
- Lingkaran melalui A (5, 0), maka:
5A + C = -25 ... (i)
- Lingkaran melalui B (0, 5), maka:
25 + 5B + C = 0
5B + C = -25 ... (ii)
- Lingkaran melalui C (-1, 0), maka:
1 – A + C = 0
-A + C = -1 ... (iii)
Eliminasi (i) dan (iii)
A = -4
Subtitusikan A = -4, pada persamaan –A + C = -1
-(-4) + C = -1
C = -5
Subtitusikan C = -5 pada persamaan 5B + C = -25
5B + (-5) = -25
5B = -20
B = -4
Sehingga persamaan lingkarannya menjadi:
Jari-jarinya:
r = √13
Jawaban: C
25. Salah satu garis singgung yang bersudut 120 derajat terhadap sumbu x konkret pada bulat dengan ujung diameter di titik (7, 6) dan (1, -2) ialah ...
a. y = -x√3 + 4√3 + 12
b. y = -x√3 - 4√3 + 8
c. y = -x√3 + 4√3 + 8
d. y = -x√3 - 4√3 - 8
e y = -x√3 + 4√3 + 22
Pembahasan:
Jari-jari:
Titik pusat:
Persamaan lingkarannya:
Persamaan garis singgung lingkaran:
...(i)Perhatikan gambar garis singgung yang dimaksud:
Berdasarkan gambar di atas, gradien garis yang dimaksud ialah y/x = - √3 /1 = - √3
Maka persamaan garis singgungnya (i) menjadi:
y = - x√3 + 4 √3 ± 5√4 + 2
y = - x√3 + 4 √3 ± 10 + 2
y = - x√3 + 4 √3 ± 10 + 2
y = - x√3 + 4 √3 + 10 + 2 = - x√3 + 4 √3 + 12
y = - x√3 + 4 √3 - 10 + 2 = - x√3 + 4 √3 - 8
Jawaban: A
Gimana nih adik-adik? sehabis mencar ilmu bersama kakak, makin paham atau makin galau nih? hehehe... biar bermanfaat ya, jangan putus-putus latihannya...
Post a Comment for "Contoh Soal Dan Pembahasan Ihwal Persamaan Bulat Sma"